728x90
반응형
Counting Sort?
counting sort는 data의 수를 count 해서 정렬하는 방법이다.
특징
- O(n+k): k 는 정렬할 숫자 중에 제일 큰값.
- 배열의 크기가 아닌 최대값의 영향을 받는다.
- 서로 비교를 하지 않고 숫자를 세어 정렬하는 방식.
- 최대값에 따라 영향을 받기 때문에 작은 범위에서 효율적이다.
- stable한 알고리즘이다. 입력에 동일한 값이 있을때 먼저 나오는 값이 출력에서도 먼저 나온다
분석
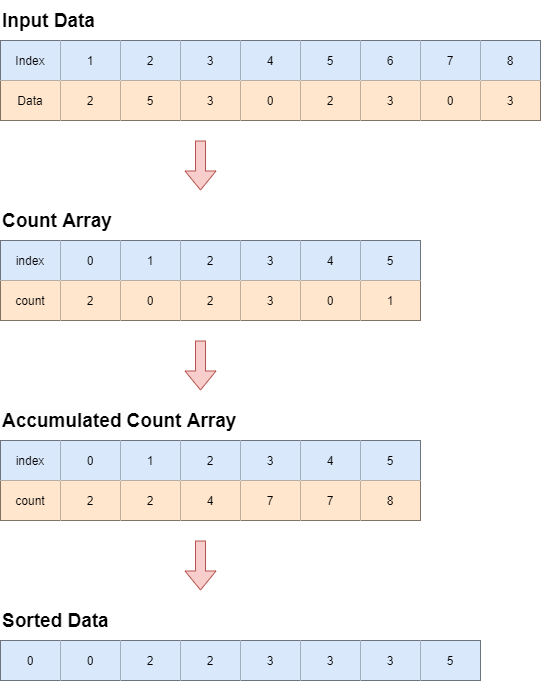
1. 데이터들의 숫자를 카운트한다.
2. 카운트 된 숫자를 출력한다.

구현
public class CountingSort {
public static void main(String[] args) {
int maxCount = 30;
int[] arrayA = {2,5,3,0,2,3,0,3};
int[] count = new int [maxCount];
for(int i = 0; i < arrayA.length; i++)
{
count[arrayA[i]]++;
}
for(int i = 0; i <maxCount; i++)
{
for(int j = 0; j < count[i]; j++) {
System.out.print(i+",");
}
}
}
}
누적합을 이용한 정렬
분석
앞서 구한 count를 누적한다.
누적한 값을 인데스 위치로 한다.
해당 위치에 값을 정렬하면 count의 인덱스 값을 줄여나간다.
구현
public class countingsort {
public static void main(String[] args) {
int maxCount = 30;
int maxValue = 5;
int[] arrayA = {2,5,3,0,2,3,0,3};
int[] count = new int [maxCount];
int[] resultArray = new int[maxCount];
for(int i = 0; i < arrayA.length; i++)
{
count[arrayA[i]]++;
}
for(int i = 1; i <= maxValue; i++)
{
count[i] += count[i-1];
}
for(int i = 0; i < 6; i++)
{
System.out.print(count[i]+",");
}
System.out.println();
for(int i = arrayA.length-1; i >= 0; i--)
{
resultArray[count[arrayA[i]]] = arrayA[i];
count[arrayA[i]]--;
}
for(int i = 1; i <= arrayA.length; i++)
{
System.out.print(resultArray[i]+",");
}
}
}
728x90
반응형
'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Binary Search Tree - Search (1) | 2021.06.08 |
|---|---|
| [Algorithm] Binary Search Tree - Insert (0) | 2021.06.08 |
| [Algorithm] Max heapify 구현과 이론 (0) | 2021.05.04 |
| [Algorithm] 병합정렬(merger sort) (0) | 2021.04.13 |
| [Algorithm] 조합 구현 (0) | 2021.04.11 |





댓글