Binary Search Tree 의 Delete구현
지금 까지 Binary Search Tree의 정의, Insert, Search, Successor, Predecessor 에 대해서 알아봤다.
아래에 링크가 있으니 처음부터 보면 도움이 될것이라 생각합니다.
Delete 구현
- delet를 구현할때 다음과 같은 사항을 고려해야한다.
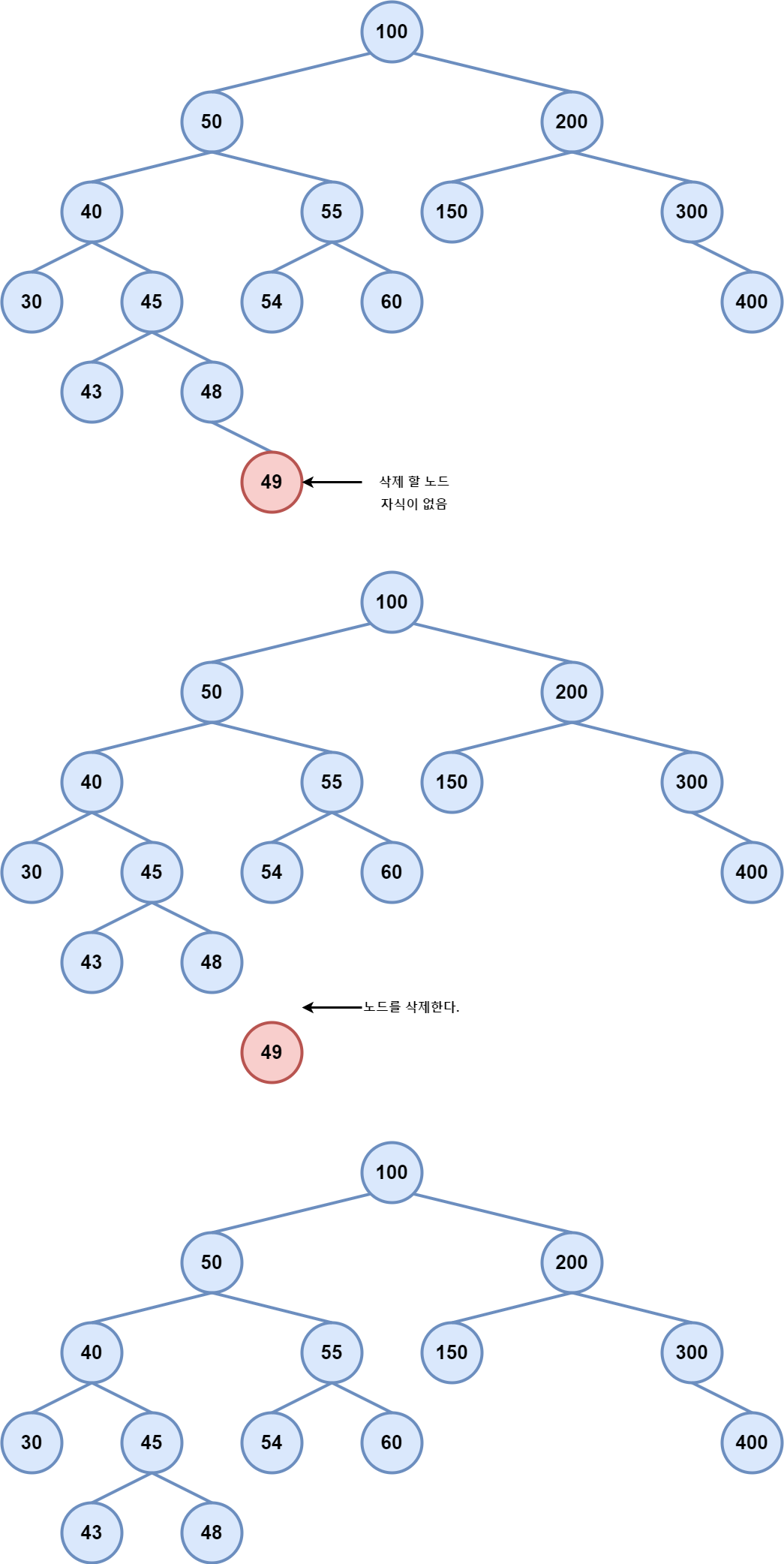
- 삭제할 노드의 자식이 아예 없을때
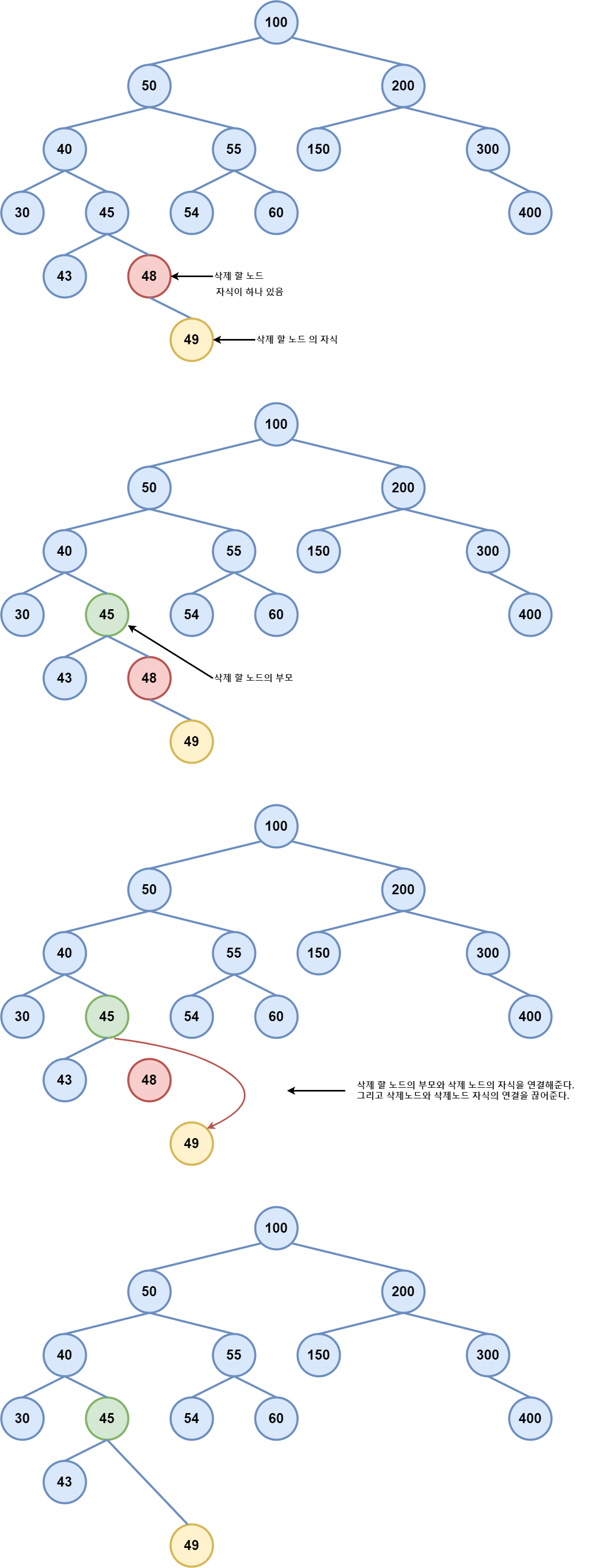
- 삭제할 노드의 자식이 하나만 있을때
- 삭제할 노도의 자식이 둘다 있을때
왜 고려해야 될까?
우리는 Insert 할때 규칙을 만들어서 Binary Search Tree를 구현하였다.
그렇기 때문에 규칙을 유지해 가면서 Tree를 삭제해야 된다.
삭제 노드의 자식이 아예 없을때
제일 간단하다 그냥 삭제노드와 삭제노드의 부모와 연결을 끊어준다.
!! 단 C++ 일 경우 메모리를 반환해주는 코드를 넣어야 한다.
삭제 노드의 자식이 하나 있는경우
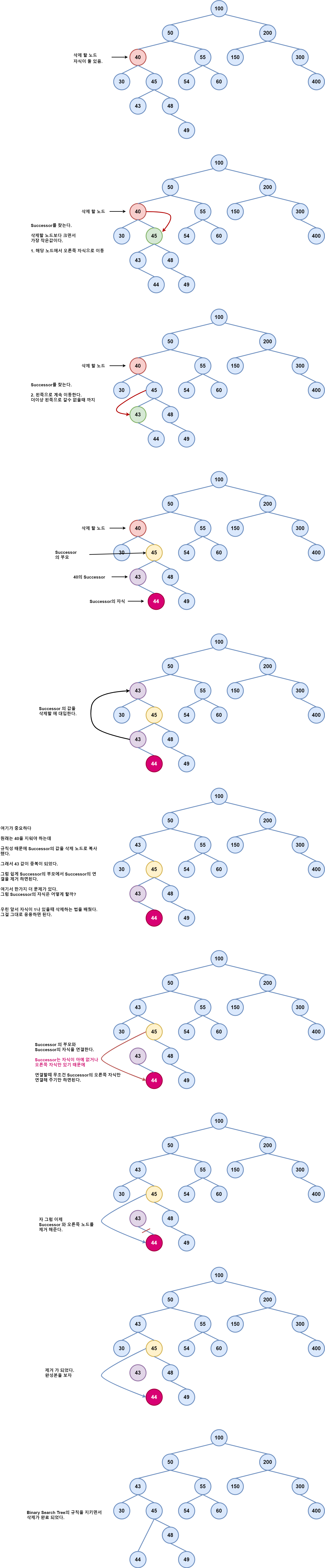
삭제 노드의 자식이 둘이 있는 경우 !!!!제일 복잡하니 천천히 이해해 가면서 보자!!!!
Successor 를 이용하여 삭제하는 방법으로 설명하겠습니다.
그림이 많아 보실때 확대해 보시면 편할것 같습니다.
1. 삭제할 노드를 찾는다.
2. 규칙을 유지 하기 위해서 삭제할 노드의 Successor 를 찾는다.
3. 찾은 Successor 의 자식이 있다면 Successor 의 부모와 Successor 의 자식을 연결해 준다. 없으면 생략
4. Successor의 부모와 Successor의 관계를 끊어 준다.
5. 중요포인트 Successor 는 자식이 하나 이거나 아예 없을 수가 있다 그렇기 때문에 자식이 하나 거나 없는 경우로 생각하면 된다
코드
public boolean removeNode(int data) {
if (rootNode == null) {
System.out.println("Can not find node");
return false;
}
Node head = rootNode;
Node parent = null;
boolean isLeftLocation = false;
while(head.getData() != data) {
parent = head;
if (head.getData() < data) {
head = head.right;
isLeftLocation = false;
} else {
head = head.left;
isLeftLocation = true;
}
if (head == null) {
System.out.println("Can not find node");
break;
}
}
if (head == null) {
return false;
}
Node targetNode = head;
Node replaceNode = null;
if (targetNode.left == null && targetNode.right == null) {
if (isLeftLocation) {
parent.left = null;
} else {
parent.right = null;
}
} else if (targetNode.left == null) {
replaceNode = targetNode.right;
if (isLeftLocation) {
parent.left = replaceNode;
} else {
parent.right = replaceNode;
}
} else if (targetNode.right == null) {
replaceNode = targetNode.left;
if (isLeftLocation) {
parent.left = replaceNode;
} else {
parent.right = replaceNode;
}
} else {
Node successor = getSuccessor(targetNode, false);
targetNode.setData(successor.getData());
}
return true;
}
public Node getSuccessor(Node node, boolean findMode) {
if (node == null)
{
System.out.println("Node is NULL");
return node;
}
if (node.right == null) {
System.out.println("Cannot find successor");
return node;
}
Node successorNode = node.right;
Node parentNode = node;
while (successorNode.left != null) {
parentNode = successorNode;
successorNode = successorNode.left;
}
if (!findMode) {
parentNode.left = successorNode.right;
}
return successorNode;
}
public Node getPredecessor(Node node, boolean findMode) {
if (node == null)
{
System.out.println("Node is NULL");
return node;
}
if (node.left == null) {
System.out.println("Cannot find predecessor");
return node;
}
Node predecessorNode = node.left;
Node parentNode = node;
while (predecessorNode.right != null) {
parentNode = predecessorNode;
predecessorNode = predecessorNode.right;
}
if (!findMode) {
parentNode.right = predecessorNode.left;
}
return predecessorNode;
}
마치면서....
드디어 Insert, Search, Successor, Predecessor 가 끝났다 구현과 공부하는 것보다
설명하면서 그림많드는게 시간이 제일 오래 걸렸다.
틀린부분도 있으니 혹시나 발견하시면 댓글 부탁드립니다.
바로 수정하겠습니다.
선행학습
https://vprog1215.tistory.com/72
Binary Search Tree - Insert
Binary Search Tree 특징 자식을 최대 2개만 가질수 있는 트리이다. root 의 왼쪽값은 root 의 값보다 작다. root 의 오른쪽 값은 root의 값보다 크다. Insert, Search, Delete, Successor, Predecessor 을 구현한..
vprog1215.tistory.com
https://vprog1215.tistory.com/73
Binary Search Tree - Search
Binary Search Tree 의 Search 구현 앞에서 Binary Search Tree의 정의와 insert를 구현을 해봤다. 이번에는 Search를 알아보고 구현해보자. https://vprog1215.tistory.com/72 Binary Search Tree - Insert Binar..
vprog1215.tistory.com
https://vprog1215.tistory.com/74
Binary Search Tree - Successor, Predecessor
Successor, Predecessor 지금 까지 Binary Search Tree의 정의, Insert, Search에 대해서 알아봤다. https://vprog1215.tistory.com/72 Binary Search Tree - Insert Binary Search Tree 특징 자식을 최대 2개만..
vprog1215.tistory.com
전체코드
구현코드:
https://github.com/rnrl1215/algorithm-base/tree/master/src/main/java/algorithm/binarysearchtree
테스트코드:
https://github.com/rnrl1215/algorithm-base/blob/master/src/test/java/BinarySearchNodeTest.java
'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Graph (0) | 2021.07.21 |
|---|---|
| [Algorithm] Binary Search Tree - Tree traversal (0) | 2021.06.10 |
| [Algorithm] Binary Search Tree - Successor, Predecessor (0) | 2021.06.08 |
| [Algorithm] Binary Search Tree - Search (1) | 2021.06.08 |
| [Algorithm] Binary Search Tree - Insert (0) | 2021.06.08 |






댓글