Kruskal
MST를 만드는 알고리즘 입니다.
적은 비용으로 노드를 연결하는 것이 핵심입니다.
Kruskal 알고리즘을 구현하기전 MST 를 알아야 합니다.
맨아래 링크를 참조해주시면 됩니다.
알고리즘 순서
- 에지들을 오름 차순으로 정렬한다.
- 에지들을 그 순서대로 하나씩 택한다.
- 싸이클 검사를 한다.
- 선택된 에지의 수가 n-1 개의 에지가 선택되면 종료한다.
눈으로 한번 보면 편합니다.
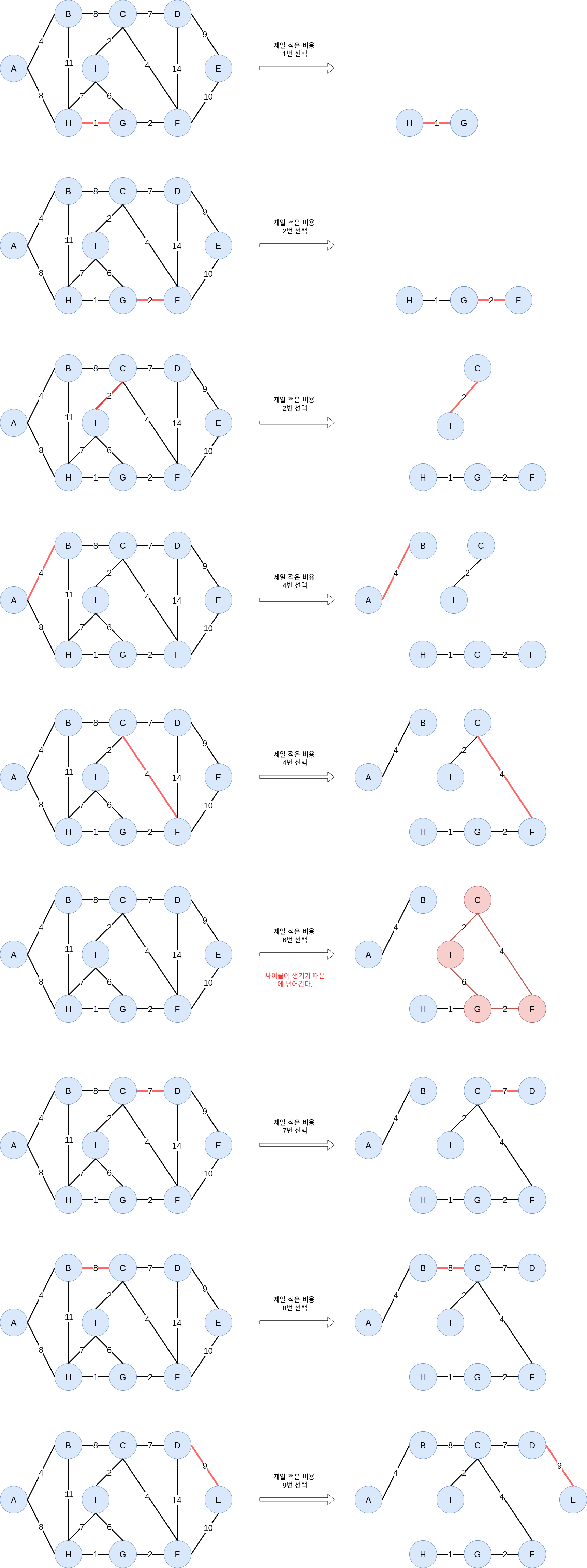
싸이클을 검사하는 방법
- 위에서 싸이클이 생겼을때 우리는 선택된 엣지를 추가 하지 않고 그냥 넘어 갔습니다.
- 집합을 사용하여 어떻게 싸이클을 검사하는지 파악해 보겠습니다.
처음 모든 노드들을 집합으로 만듭니다.
{A} {B} {C} {D} {E} {F} {G} {H} {I}
집합에 선택된 노드를 넣어 준다.
- 선택한 간선을 넣어 줄때 임의의 집합 A에 노드를 합쳐 줍니다.
예를 들어 A-B 를 연결하는 간선을 추가 해주면
A = {A, B} 이렇게 추가가 됩니다. - 어느단계 까지 오면 다음과 같은 그림이 만들어 지게 됩니다.
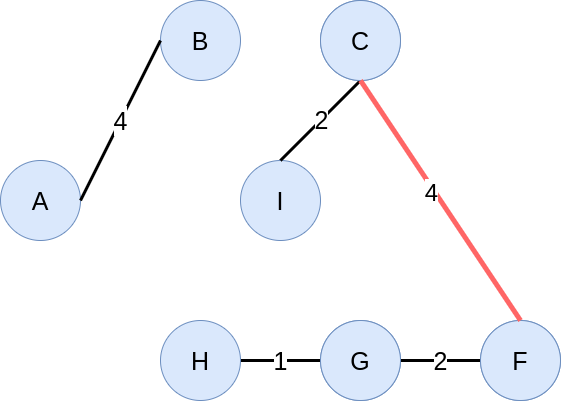
집합 A
{A, B}
집합 B
{C,F,G,H,I}
집합을 통해 싸이클을 검사한다.
- 여기서 I-G 를 택하여 그래프에 추가하면 싸이클이 생기게 됩니다.

- 다음과 같이 집합을 이용하여 검사하면 싸이클을 피할수 있습니다.
- 선택한 노드 I-G 가 동일한 집합에 속해 있는지 판단합니다.
- 만일 동일한 집합에 두 노드가 속해 있다면 싸이클이 생기게 됩니다.
- 두 노드가 다른 집합에 있다면 안전하게 연결 하면 됩니다.
집합 A
{A, B}
집합 B
{C,F,G,H,I}
- I G 는 집합 B에 모두 들어 있기 때문에 추가하게 되면 싸이클이 생깁니다.
- 하지만 B-C 를 봤을때 B 는 A 집합에 속에 있고 C 는 B 집합에 속해 있기 때문에
연결 되어도 싸이클이 생기지 않습니다.
집합을 표현하는 방법
- 위에서 집합으로 그래프를 만들고 싸이클을 검사하는 방법을 보았습니다.
- 그럼 어떻게 집합을 표현하는지 살펴 보겠습니다.
- 트리구조로 집합을 표현합니다.
그 이유는 싸이클을 검사할때 부모만 찾으면 쉽게 검사 할수 있기 때문입니다.
트리로 표현
- 집합을 트리로 표현합니다.
- 여기서 좀 다른점은 보통 Root 에서 뻗어 나가지만
여기서는 자식에서 위로 뻗어나가는 방식으로 만듭니다. - A 의 부모는 A 자신이기 때문에 스스로를 부모라고 합니다.

- 그림처럼 쉽게 집합에 포함되었는지 찾을수 있습니다
- 위에서 G-I 를 연결 할때 트리로 검사해봅니다.
G 의 부모 = C
I 의 부모 = C- 부모가 동일 하기 때문에 같은 집합에 속해있다고 판단할수 있습니다.
배열로 표현
- 사실 트리로 굳이 표현할 필요가 없습니다.
- 왜냐면 배열로도 충분히 부모를 찾을수 있기 때문 입니다.
| 자신 | A | B | C | D | E | F | G | H | I |
| 부모 | A | A | C | D | E | C | F | G | C |
구현
구현부
package com.company;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.List;
public class Kruskal {
// Edge 정의
static class Edge implements Comparable<Edge> {
int u;
int v;
int weight;
// 정렬을 위한 비교함수
@Override
public int compareTo(Edge n) {
return this.weight - n.weight;
}
public Edge(int u, int v, int weight) {
this.u = u;
this.v = v;
this.weight = weight;
}
}
// Edge 리스트
public List<Edge> nodes = new ArrayList<Edge>();
// 각각의 노드에 대한 부모를 저장
private int []parent;
// 부모가 가지고 있는 노드의 수정의
private int []nodeSize;
public void setNode(int u, int v, int weight) {
Edge edge = new Edge(u, v, weight);
nodes.add(edge);
}
// 싸이클 검사
public boolean isCycle(int u, int v) {
int xParent = findSet(u);
int yParent = findSet(v);
boolean ret = false;
if (xParent == yParent) {
ret = true;
} else {
ret = false;
}
return ret;
}
// 해당 노드의 부모를 찾는다.
public int findSet(int node) {
while (node != parent[node]) {
parent[node] = parent[parent[node]];
node = parent[node];
}
return node;
}
// 노드를 합친다.
// 각각 노드의 부모를 찾는다.
// 속도 개선을 위해 부모의 자식수를 비교한다.
// 자식이 많은 쪽에 적은 쪽이 다시 자식이 된다.
public void weightUnion(int u, int v) {
int uParent = findSet(u);
int vParent = findSet(v);
if (nodeSize[uParent] <= nodeSize[vParent]) {
parent[vParent] = uParent;
nodeSize[vParent] = nodeSize[vParent]+nodeSize[uParent];
}
}
// 크루스칼 알고리즘 수행
public int runKruskal(int size) {
// 낮은 순으로 정렬
Collections.sort(nodes);
size = size+1;
// 부모사이즈와 부모 초기화
parent = new int[size];
nodeSize = new int[size];
for(int i = 0; i <size; i++) {
parent[i] = i;
nodeSize[i] =1;
}
int sum = 0;
for(Edge node : nodes) {
// 싸이클이 존재 하지않으면 안전하다.
if(!isCycle(node.u, node.v)) {
// 두노드를 합친다.
weightUnion(node.u,node.v);
System.out.println("U:"+node.u+" V:"+node.v+ " weight:" +node.weight);
sum += node.weight;
}
}
System.out.println(sum);
return 1;
}
}
수행부
public class Main {
public static void main(String[] args) {
// write your code her
Kruskal kruskal= new Kruskal();
kruskal.setNode(0,1,4);
kruskal.setNode(0,7,8);
kruskal.setNode(1,2,8);
kruskal.setNode(1,7,11);
kruskal.setNode(2,3,7);
kruskal.setNode(2,8,2);
kruskal.setNode(2,5,4);
kruskal.setNode(3,5,14);
kruskal.setNode(3,4,9);
kruskal.setNode(4,5,10);
kruskal.setNode(5,6,2);
kruskal.setNode(6,8,6);
kruskal.setNode(6,8,6);
kruskal.setNode(6,7,1);
kruskal.setNode(7,8,7);
kruskal.runKruskal(8);
}
}
결과
U:6 V:7 weight:1
U:2 V:8 weight:2
U:5 V:6 weight:2
U:0 V:1 weight:4
U:2 V:5 weight:4
U:2 V:3 weight:7
U:0 V:7 weight:8
U:3 V:4 weight:9
37
전체코드
https://github.com/rnrl1215/algorithm-study/blob/main/src/main/java/algorithm/kruskal/Kruskal.java
GitHub - rnrl1215/algorithm-study
Contribute to rnrl1215/algorithm-study development by creating an account on GitHub.
github.com
테스트코드:
https://github.com/rnrl1215/algorithm-study/blob/main/src/test/java/KurskalTest.java
GitHub - rnrl1215/algorithm-study
Contribute to rnrl1215/algorithm-study development by creating an account on GitHub.
github.com
MST 란?
https://vprog1215.tistory.com/155
[Algorithm] MST(Minimum Spanning Tree)
MST 란? Minimum Spanning Tree 최소 신장 트리이다. 간선의 가중치를 고려 하여 최소 Spanning Tree 를 만든다. 싸이클이 없는 연결된 무방향 그래프를 트리 라고 한다. 모든 정점들이 연결이 되어 있어야
vprog1215.tistory.com
'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Quick Sort (0) | 2021.08.30 |
|---|---|
| [Algorithm] 탐색문제 재귀로 구현해보기 (1) | 2021.08.16 |
| [Algorithm] MST(Minimum Spanning Tree) (0) | 2021.08.10 |
| [Algorithm] DAG(Directed Acyclic Graph) (0) | 2021.08.03 |
| [Algorithm] Graph Traversal BFS, DFS (1) | 2021.07.22 |





댓글