728x90
반응형
Shortest Path
- 최단거리 알고리즘에 대해서 알아보고 공부해 본다.
최단경로의 특징
- 가중치 그래프가 주어진다.
- 경로의 길이는 모든 에지의 가중치 합이다.
- 최단 경로의 부분경로도 최단경로다.
- 최단 경로 안에있는 모든 경로는 최단 경로이다.
- 최단경로는 싸이클을 포함하지 않는다.
- N 개의 노드가 있으면 순환이 없어야 하므로 엣지의 개수는 N-1 이다.
최단경로의 문제종류
single-source
- 하나의 출발 노드 s로부터 다른 모든 노드까지의 최단 경로를 찾는것
- 가장 유용한 방식이다.
- ex) dijkstra 알고리즘이 있다.
single-destination
- 목적지가 주어지고 모든 노드로부터 목적지 까지의 최단거리
- single-source 와 동일하다.
single-pair
- 주어진 하나의 출발 노드 s로 부터 하나의 목적지 노드 t 까지의 최단 경로를 찾는것
- 최악의 경우 시간복잡도에서 single-source 문제보다 나은 알고리즘이 없다.
all-pairs
- 모든 노드 쌍에 대해 최단경로 찾기
음수 가중치
- 그래프에 음수가중치가 있을때 해결할수 있는 알고리즘이 있고
- 해결 할 수 없는 알고리즘이 있다.
- 다익스트라 인 경우 음수가중치가 없다는 전제하에 구현 되었기 때문에
적용하지 못한다.
single-source 최단 경로문제
- 다음과 같은 용어들이 있다.
- d[v]: s 에서 부터 v 까지 가는 가장 짧은 경로길이
- π[v]:s 에서 부터 v 까지 노드중 v 의 직전노드
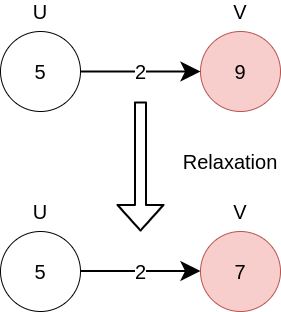
Relaxation
현재 주어진 경로보다 더 짧은 경로가 있으면 값을 업데이트 해주는 연산이다.
예를 들어 다음과 같은 그림을 보자
Relaxation 전
시작 노드에서 노드 U 까지 오는데 걸린 최단 거리는 5이다.
시작 노드에서 노드 V 까지 오는데 걸린 최단 거리는 9이다
하지만 U 에서 V 로 갈때 걸리는 길이는 7(d[v] = d[u] + w(u,v)) 이다
기존 9보다 작은 값이니 더 작은 값을 업데이트 해준다.
Relaxation 후
노드 U 까지 오는데 걸린 최단 거리는 5이다.
노드 V 까지 오는데 걸린 최단 거리는 7이다
Relaxation 슈도코드
Relax(u,v,w)
// v의 계산된 거리보다 지금의 거리가 더 가까우면 값을 업데이트한다.
if(d[v] > d[u] + w(u,v))
then d[v]<-d[u]+w(u,v)
pi[v] <- u
728x90
반응형
'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Shortest Path 3: Dijkstra (0) | 2021.09.29 |
|---|---|
| [Algorithm] Shortest Path 2: Bellman-Ford (0) | 2021.09.28 |
| [Algorithm] Prim (0) | 2021.09.14 |
| [Algorithm] Quick Sort (0) | 2021.08.30 |
| [Algorithm] 탐색문제 재귀로 구현해보기 (1) | 2021.08.16 |






댓글