728x90
반응형
Bellman-Ford 알고리즘
- 벨만포드 알고리즘은 최단거리를 찾을때 사용한다.
- 다익스트라와 차이점이 있다면 음수의 가중치를 취급한다는 것이다.
- 하지만 속도 면에서는 다익스트라가 빠르다.
Bellman-Ford 특징
- 음수의 가중치를 처리할수 있다.
- 모든 노드에 대해 Relaxation 을 수행한다.
수행단계
- 모든 노드를 선택해 최단거리를 구한다.
- S 에서 모든 노드를 방문하면서 relaxtion 연산을 수행한다.
- 그리고 다음노드를 선택하고 또 모든 노드를 relaxtion 연산을 수행한다.
- n-1 노드만큼 반복해준다.
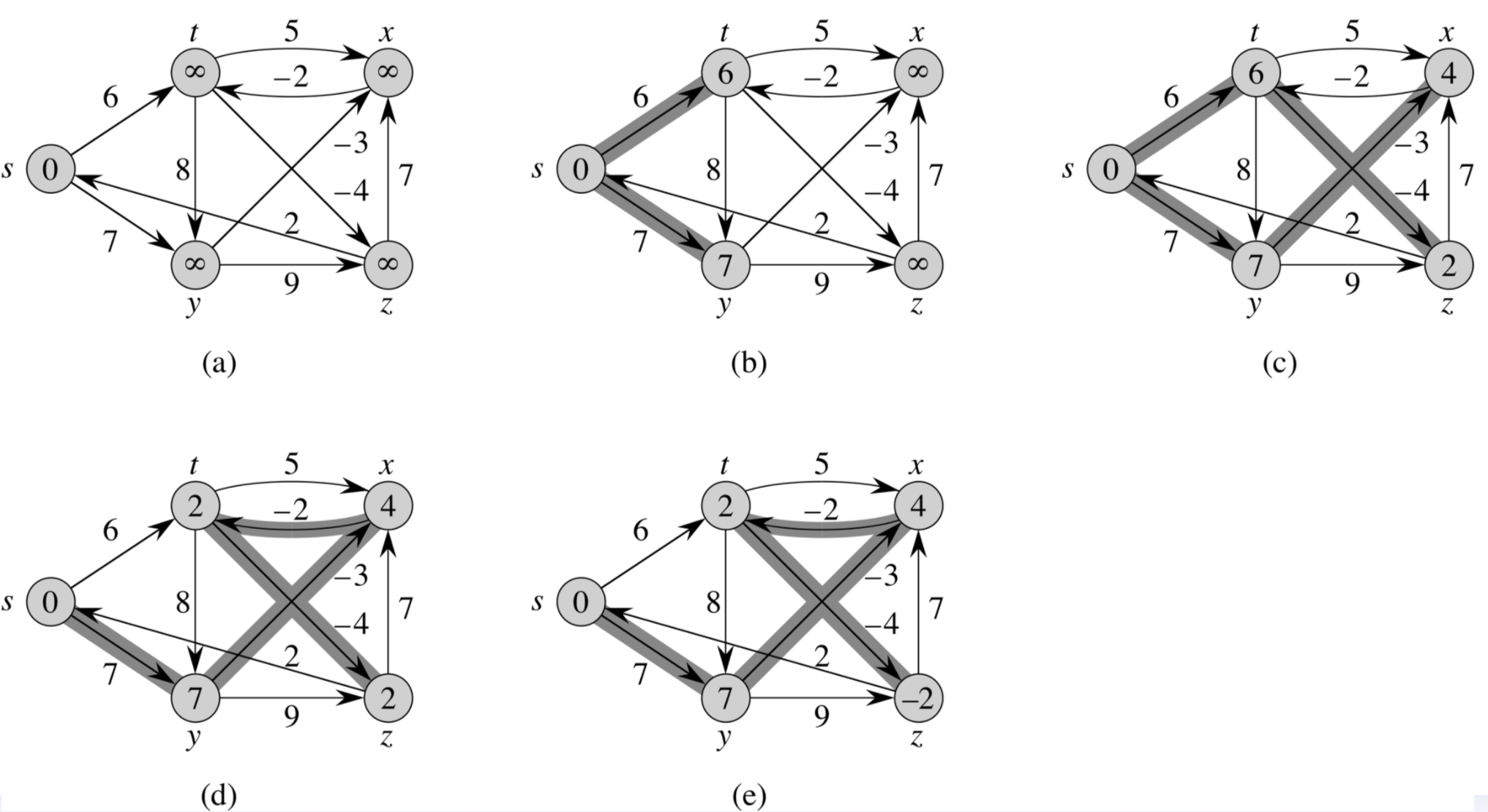
구현
package algorithm.bellmanford;
import java.util.ArrayList;
import java.util.List;
public class BellmanFord {
List<List<Edge>> graph = new ArrayList<>();
int []dist;
int maxValue = 987654321;
static class Edge {
int u; // 시작 노드
int v; // 끝 노드
int w; // 가중치
public Edge(int u, int v, int w) {
this.u = u;
this.v = v;
this.w = w;
}
}
public BellmanFord(int count, int start) {
dist = new int[count];
for(int i = 0; i <= count; i++) { // 주어진 노드 수만큼 graph 초기화
graph.add(new ArrayList<Edge>());
}
dist[start] = 0;
for(int i = 1; i < count; i++) {
dist[i] = maxValue; // 최대값으로 각노드의 거리 초기화
}
}
public void addEdge(int u, int v, int w) {
graph.get(u).add(new Edge(u,v,w)); // 단방향 그래프 생성
}
public void relax(int u, int v, int w) { // 노드에 대해 relax 연산수행
if(dist[u] == maxValue) { // 방문안한 노드는 무시
return;
}
if(dist[v] > dist[u]+w) { // delta 값 업데이트
dist[v] = dist[u]+w;
}
}
public boolean hasMinusCycle() { // 마이너스 순환 싸이클이 있는지 체크
boolean ret = true;
for(int j = 0; j < graph.size(); j++) {
for (Edge edge : graph.get(j)) {
if (dist[edge.v] > dist[edge.u] + edge.w) {
ret = false;
break;
}
}
}
return ret;
}
public boolean runBellmanFord() {
for (int i = 0; i < graph.size() - 1; i++) {
for (int j = 0; j < graph.size(); j++) {
for (Edge edge : graph.get(j)) {
relax(edge.u, edge.v, edge.w);
}
}
}
boolean ret = true;
ret = hasMinusCycle();
return ret;
}
public void printDistance() {
for(int i = 0; i <dist.length; i++) {
System.out.println("delta of node("+i+") is "+dist[i]);
}
}
}
테스트
import algorithm.bellmanford.BellmanFord;
public class BellmanFordTest {
public static void main(String[] args) {
try {
BellmanFord bellmanFord = new BellmanFord(5,0);
bellmanFord.addEdge(0, 1, 6);
bellmanFord.addEdge(0, 2, 7);
bellmanFord.addEdge(1, 3, 5);
bellmanFord.addEdge(1, 2, 8);
bellmanFord.addEdge(1, 4, -4);
bellmanFord.addEdge(2, 3, -3);
bellmanFord.addEdge(2, 4, 9);
bellmanFord.addEdge(3, 1, -2);
bellmanFord.addEdge(4, 3, 7);
bellmanFord.addEdge(4, 0, 2);
if (bellmanFord.runBellmanFord()) {
System.out.println("SUCCESS");
bellmanFord.printDistance();
} else {
System.out.println("음수싸이클 발생");
bellmanFord.printDistance();
}
} catch (Exception e) {
System.out.println(e.getMessage());
}
}
}
결과
delta of node(0) is 0
delta of node(1) is 2
delta of node(2) is 7
delta of node(3) is 4
delta of node(4) is -2728x90
반응형
'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Shortest Path 4: Floyd-Warshall (2) | 2021.10.01 |
|---|---|
| [Algorithm] Shortest Path 3: Dijkstra (0) | 2021.09.29 |
| [Algorithm] Shortest Path 1: 개념 (0) | 2021.09.28 |
| [Algorithm] Prim (0) | 2021.09.14 |
| [Algorithm] Quick Sort (0) | 2021.08.30 |






댓글