Floyd-Warshall
최단 경로를 찾는 알고리즘중 하나이다.
모든 쌍들간의 최단 경로 길이를 구한다.
Floyd-Warshall 특징
노드의 개수가 N 개이면 노드들의 번호는 1~N 이어야 한다.
Floyd-Warshall 동작 방식
i~j 까지 가는데 최단 길이를 찾는 다고 가정해보자.
k 라는 노드를 거쳐 갈수도 안 거쳐 갈 수도 있다.
Floyd-Warshall 구현하기 위한 필요한 값들
d k [i,j]:
- i~j 까지의 거리 값이다 1~K 까지 속한 노드들만 거쳐간다.
- 즉 K+1 은 지날수 없다. - d k [i,j] 를 구하는 공식은 다음과 같다.
- d k [i,j] = min(d k-1 [i,j], d k-1 [i,k]+d k-1 [k,j])
- 당황하지 말자 아래에서 설명하려 한다.
d k [i,j] = min(d k-1 [i,j], d k-1 [i,k]+d k-1 [k,j])
- i~k 를 가는 거리와 k~j 까지 거리를 더하면 d k-1 [i,k]+d k-1 [k,j] 된다.
- i~j 로 바로 가는 거리는 d k-1 [i,j] 가 된다 둘중 최소 값을 고르면 된다.

d 0[i,j]
- i,j 를 연결 하는 에지가 있으면 가중치값을 가지고 그렇지 않으면 무한 값을 가진다.
d n [i,j]
- k 가 n 이라는 말이다.
- 1~n 사이의 노드를 지날수 있다는 것이다.
- 즉 어떤 경로를 지나도 상관이 없다.
- 우리가 최종적으로 구하는 값이다.
Floyd-Warshall 슈도코드
3차원 배열이 필요한 코드
- i, j, k 에 대한 값을 저장하려면 3원 배열이 필요하다
FolydWarshall(G)
{
for i <- 1 to n
for j <-1 to n
d 0 [i,k] <- w(i,j) // 초기화 i,j 로 가는길이 있으면 가중치 그렇 지 않으면 무한으로 초기화
for k <- 1 to n // k 를 1씩 증가하면서 아래 모든 i,j 쌍에 대해 거리를 구하면 된다.
for i <- 1 to n
for j <- 1 to n
d k [i,j] <- min{ d k-1 [i,j], d k-1 [i,k] + d k-1 [k,j] }; 시간 복잡도는 O(n^3)
}
2차원 배열이 필요한 코드
FolydWarshall(G)
{
for i <- 1 to n
for j <- 1 to n
d 0 [i,k] <- w(i,j) // 초기화 i,j 로 가는길이 있으면 가중치 그렇 지 않으면 무한으로 초기화
for k <- 1 to n // k 를 1씩 증가하면서 아래 모든 i,j 쌍에 대해 거리를 구하면 된다.
for i <- 1 to n
for j <- 1 to n
d k [i,j] <- min{ d k-1 [i,j], d k-1 [i,k] + d k-1 [k,j] };
}
- 3차원에서 2차배열로 좀 간편해 졌다 그러면 배열 d 에 값을 덮어 써도 상관없는가?
- 상관없다 distane 를 구하기 위해 사용되는 배열이므로 기존값을 기억할 이유가 없다.
- 업데이트 되면 그 값을 쓰면된다.
최단 거리의 노드들을 구하는 코드
최단 거리만 구하는 문제보다 최단 거리 경로 노드들을 구하는 문제가 보통이다.
그렇기 때문에 최단 경로를 저장하는 배열도 필요하다.
FolydWarshall(G)
{
for i <- 1 to n
for j <-1 to n
d[i,k] <- w(i,j) // 초기화 i,j 로 가는길이 있으면 가중치 그렇 지 않으면 무한으로 초기화
pi[i,j] <- NIL
for k <- 1 to n // k 를 1씩 증가하면서 아래 모든 i,j 쌍에 대해 거리를 구하면 된다.
for i <- 1 to n
for j <- 1 to n
if( d[i,j] > d[i,k]+d[k,j] // i ~ j 까지 가는 것은 node k 를 지나지 않는 것이 더 좋다.
d[i,j] <- d[i,k]+d[k,j]
pi[i,j] <- k
}
// s 와 t 를 제외한 경로 노드를 출력하는 코드
print-Path(s, t, pi) {
if pi[s,t] != NIL then
return
print-path(s,pi[s,t]);
print(pi[s,t]);
print-path(pi[s,t],t);
}
구현
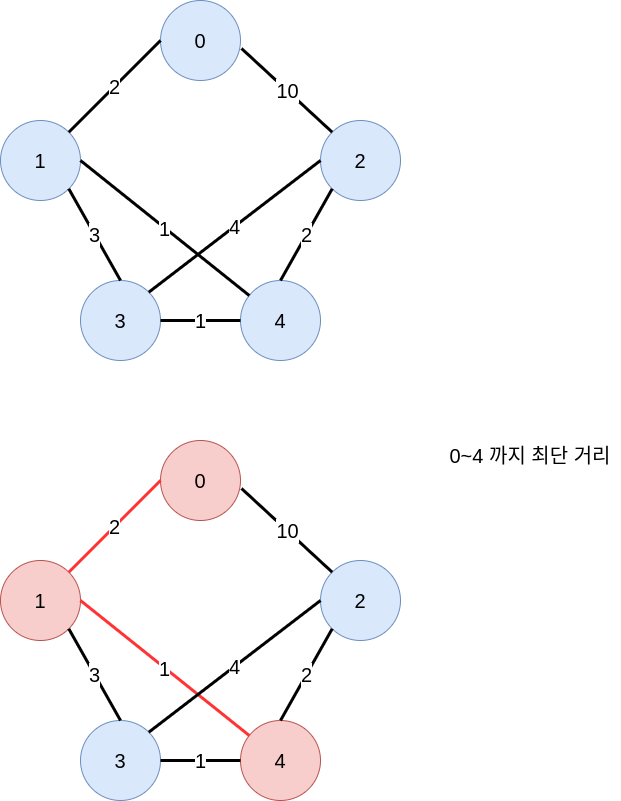
아래 그래프에서 0 번 노드에서 4번 노드의 최단거리는
0 -> 1 -> 4 이다.
구현코드
package algorithm.floydwarshall;
public class FloydWarShall {
static final int INF = 987653421;
private int [][]graph;
private int [][]pi;
private int count;
public FloydWarShall(int count) {
this.count = count;
graph = new int[count][count];
pi = new int[count][count];
for (int i = 0; i < count; i++) {
for (int j = 0; j < count; j++) {
graph[i][j] = INF;
pi[i][j] = INF;
}
}
}
public void addNode(int u, int v, int w) {
graph[u][v] = graph[v][u] = w;
}
public void runFloydWarshall() {
for (int k = 0; k < count; k++) {
for (int i = 0; i < count; i++) {
for (int j = 0; j < count; j++) {
if (graph[i][j] > graph[i][k] + graph[k][j]) {
graph[i][j] = graph[i][k] + graph[k][j];
pi[i][j] = k;
}
}
}
}
}
public void printPath(int s, int t) {
if(pi[s][t] == INF) {
return;
}
printPath(s,pi[s][t]);
System.out.println("Node: "+pi[s][t]);
printPath(pi[s][t],t);
}
}
테스트코드
import algorithm.floydwarshall.FloydWarShall;
public class FloydWarShallTest {
public static void main(String[] args) {
FloydWarShall floydWarshall = new FloydWarShall(5);
floydWarshall.addNode(0,1,2);
floydWarshall.addNode(0,2,10);
floydWarshall.addNode(1,3,3);
floydWarshall.addNode(2,3,4);
floydWarshall.addNode(2,4,2);
floydWarshall.addNode(3,4,1);
floydWarshall.addNode(4,1,1);
floydWarshall.runFloydWarshall();
System.out.println("Node: 0");
floydWarshall.printPath(0,4);
System.out.println("Node: 4");
}
}
결과
Node: 0
Node: 1
Node: 4'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Complete Binary Tree (0) | 2021.10.03 |
|---|---|
| [Algorithm] Huffman Coding 1: 개념 (1) | 2021.10.01 |
| [Algorithm] Shortest Path 3: Dijkstra (0) | 2021.09.29 |
| [Algorithm] Shortest Path 2: Bellman-Ford (0) | 2021.09.28 |
| [Algorithm] Shortest Path 1: 개념 (0) | 2021.09.28 |






댓글