728x90
반응형
Complete Binary Tree
- 완전 이진 트리라고 한다.
- 이번글에는 Insert 와 순회만 구현하려고 한다.
Complete Binary Tree 특징
- 부모는 최대 2개의 자식을 가질 수 있다.
- 마지막 레벨에서 왼쪽부터 차례대로 채워져 있는 트리다.
- 중간에 비어있는 트리가 있으면 안된다.
- 트리는 Root, Parent, Child 로 구성 되어 있다.
Complete Binary Tree
- 완전이진트리이다.
- 마지막 레벨 에 하나의 노드 만 빼고 꽉 차있다.
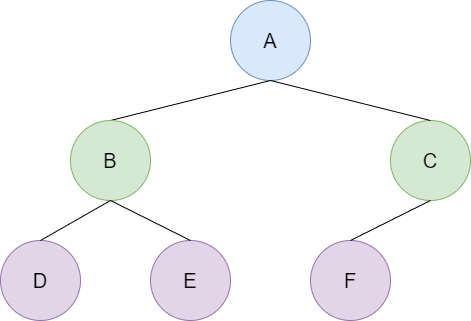
구현
- 사실 트리 구조는 노드와 insert 연산 탐색 연산이면
충분하다. - 하지만 insert 할때 순서대로 채우려면 어떻게 해야될까?
고민을좀 했다. - queue를 이용해서 다음에 채워야할 노드를 저장하고 있으면 될것 같다.
구현
구현코드
package algorithm.completebinarytree;
import java.util.LinkedList;
import java.util.Queue;
public class CompleteBinaryTree {
class Node {
public Node(char data) {
this.data = data;
}
private char data;
private Node leftNode;
private Node RightNode;
}
private Node rootNode;
public void insertNode(char data) {
if(rootNode == null) {
rootNode = new Node(data);
return;
}
Queue<Node> queue = new LinkedList<>();
queue.add(rootNode);
Node node = new Node(data);
while (true) {
Node tmpNode = queue.poll();
if(tmpNode.leftNode == null) {
tmpNode.leftNode = node;
break;
} else {
queue.add(tmpNode.leftNode);
}
if(tmpNode.RightNode == null) {
tmpNode.RightNode = new Node(data);
System.out.println("RIGHT: "+data);
break;
} else {
queue.add(tmpNode.RightNode);
}
}
}
public Node getRootNode() {
return rootNode;
}
public void preOrder(Node node) {
if(node == null) {
return;
}
System.out.println(node.data);
preOrder(node.leftNode);
preOrder(node.RightNode);
}
public void postOrder(Node node) {
if(node == null) {
return;
}
postOrder(node.leftNode);
postOrder(node.RightNode);
System.out.println(node.data);
}
public void inOrder(Node node) {
if(node == null) {
return;
}
inOrder(node.leftNode);
System.out.println(node.data);
inOrder(node.RightNode);
}
}
테스트코드
import algorithm.completebinarytree.CompleteBinaryTree;
public class CompleteBinaryTreeTest {
public static void main(String[] args) {
try {
CompleteBinaryTree completeBinaryTree = new CompleteBinaryTree();
completeBinaryTree.insertNode('A');
completeBinaryTree.insertNode('B');
completeBinaryTree.insertNode('C');
completeBinaryTree.insertNode('D');
completeBinaryTree.insertNode('E');
completeBinaryTree.insertNode('F');
System.out.println("PRE ORDER");
completeBinaryTree.preOrder(completeBinaryTree.getRootNode());
System.out.println("POST ORDER");
completeBinaryTree.postOrder(completeBinaryTree.getRootNode());
System.out.println("IN ORDER");
completeBinaryTree.inOrder(completeBinaryTree.getRootNode());
} catch (Exception e) {
System.out.println(e.getMessage());
}
}
}
728x90
반응형
'Algorithm > 알고리즘 기본' 카테고리의 다른 글
| [Algorithm] Huffman Coding 3: Decoding 예제 설명 과 구현 (0) | 2021.10.15 |
|---|---|
| [Algorithm] Huffman Coding 2: Encoding 예제 설명 과 구현 (2) | 2021.10.15 |
| [Algorithm] Huffman Coding 1: 개념 (1) | 2021.10.01 |
| [Algorithm] Shortest Path 4: Floyd-Warshall (2) | 2021.10.01 |
| [Algorithm] Shortest Path 3: Dijkstra (0) | 2021.09.29 |





댓글